tanuki- 2022-07-08 nnue-pytorch NVLAMB

tanuki- 2022-07-08 nnue-pytorch NVLAMB

実験内容

• nnue-pytorch を用いた学習で、 Optimizer を NVLAMB に変更して学習させた場合の、レーティングの変化を調べる。

棋譜生成

生成ルーチン	tanuki-棋譜生成ルーチン
評価関数	水匠5 FV_SCALE=16
1手あたりの思考	深さ最大 9 思考ノード数最大 50,000 ノード
開始局面	foodgate の 2020 年～ 2021 年の棋譜のうち、レーティング 3900 以上同士の対局の 32 手目までから 1 局面ランダムに選択し、その局面を開始局面とした ランダムムーブなし
生成局面数	10 億局面 × 8 セット
生成条件	対局は打ち切らず詰みの局面まで学習データに出力した

シャッフル条件

生成ルーチン	tanuki-シャッフルルーチン
qsearch()	あり
置換表	無効

機械学習

機械学習ルーチン	nnue-pytorch + やねうら王 https://github.com/nodchip/nnue-pytorch/tree/shogi.2022-05-23
学習モデル	halfkp_256x2-32-32
学習手法	SGD ミニバッチ法
最適化手法	NVLAMB
学習率調整手法	StepLR step=1 gamma=0.992
batch-size	16384
threads	2
num-workers	2
gpus	1
features	HalfKP
max_epoch	300
scaling (kPonanzaConstant)	361
lambda	0.5
勝敗項の教師信号	1.0

レーティング測定

対局相手	tanuki- 2022-04-01 halfkp_256x2-32-32 再実験 https://docs.google.com/document/d/1U2dtYgksApn9GYIUJEUtceE0Yc-0dfmx6kA44FopDXc/edit
思考時間	持ち時間 300 秒 + 1 手 2 秒加算
対局数	5000
同時対局数	64
ハッシュサイズ	768
開始局面	たややん互換局面集

実験結果

機械学習

レーティング測定

対局数=5000 同時対局数=64 ハッシュサイズ=768 開始手数=24 最大手数=320 開始局面ファイル=C:\Jenkins\workspace\TanukiColiseum.2022-05-02\TanukiColiseum\taya36_2020-11-06.sfen NUMAノード数=2 表示更新間隔(ms)=3600000

思考エンジン1 name=YaneuraOu NNUE 7.10 64ZEN2 TOURNAMENT author=by yaneurao exeファイル=C:\Jenkins\workspace\TanukiColiseum.2022-05-02\engine1\source\YaneuraOu-by-gcc.exe 評価関数フォルダパス=D:\hnoda\shogi\eval\tanuki-.nnue-pytorch-2022-07-06 定跡手数=256 定跡ファイル名=no_book 思考ノード数=0 思考ノード数に加える乱数(%)=0 思考ノード数の乱数を1手毎に変化させる=False 持ち時間(ms)=300000 秒読み時間(ms)=0 加算時間(ms)=2000 乱数付き思考時間(ms)=0 スレッド数=1 BookEvalDiff=30 定跡の採択率を考慮する=false 定跡の手数を無視する=false SlowMover=100 DrawValue=-2 BookEvalBlackLimit=0 BookEvalWhiteLimit=-140 FVScale1=16

思考エンジン2 name=YaneuraOu NNUE 7.10 64ZEN2 TOURNAMENT author=by yaneurao exeファイル=C:\Jenkins\workspace\TanukiColiseum.2022-05-02\engine2\source\YaneuraOu-by-gcc.exe 評価関数フォルダパス=D:\hnoda\shogi\eval\suisho5.halfkp_256x2-32-32.80G\final 定跡手数=256 定跡ファイル名=no_book 思考ノード数=0 思考ノード数に加える乱数(%)=0 思考ノード数の乱数を1手毎に変化させる=False 持ち時間(ms)=300000 秒読み時間(ms)=0 加算時間(ms)=2000 乱数付き思考時間(ms)=0 スレッド数=1 BookEvalDiff=30 定跡の採択率を考慮する=false 定跡の手数を無視する=false SlowMover=100 DrawValue=-2 BookEvalBlackLimit=0 BookEvalWhiteLimit=-140 FVScale2=16

対局数5000 先手勝ち2357(52.1%) 後手勝ち2163(47.9%) 引き分け480

engine1

勝ち1973(43.7% R-40.1 +-9.7) 先手勝ち1033(22.9%) 後手勝ち940(20.8%)

宣言勝ち83 先手宣言勝ち46 後手宣言勝ち37 先手引き分け244 後手引き分け236

engine2

勝ち2547(56.3%) 先手勝ち1324(29.3%) 後手勝ち1223(27.1%)

宣言勝ち43 先手宣言勝ち24 後手宣言勝ち19 先手引き分け236 後手引き分け244

1973,480,2547

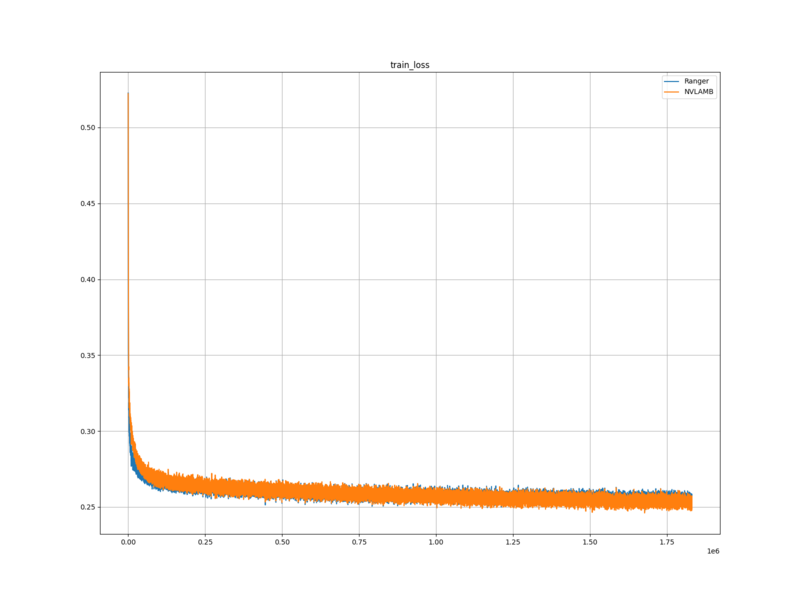
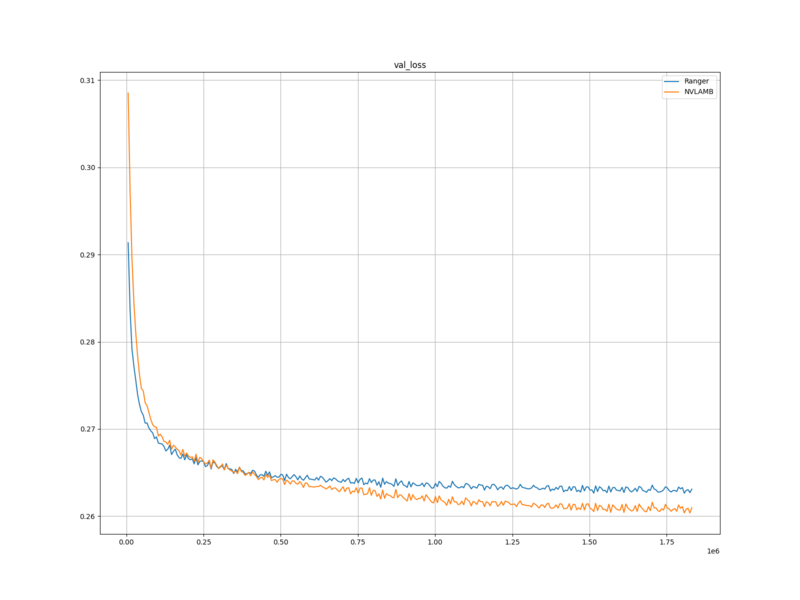
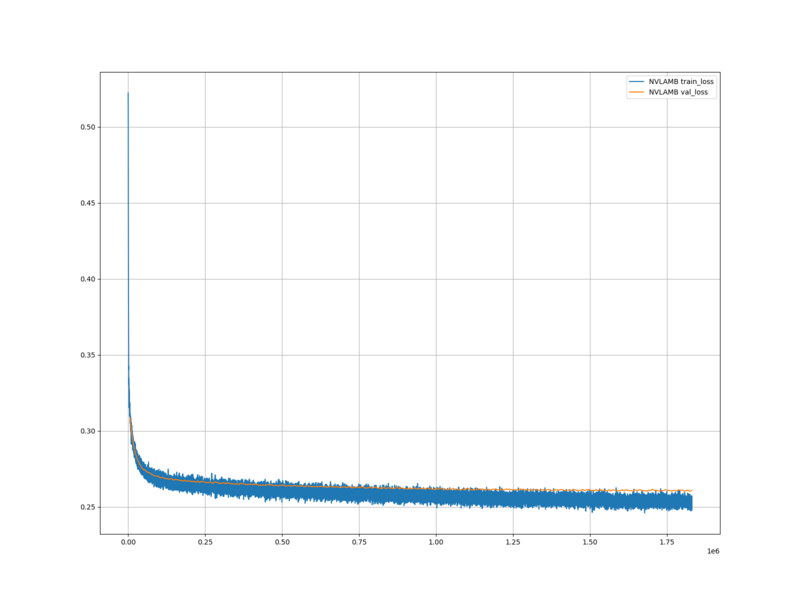
学習ロスと検証ロスは、 Ranger を使用した場合と比べ、学習し始めの頃は高かったが、最終的には低くなった。

レーティングは、比較対象の評価関数と比べて、 R-40.1 低かった。 これは Ranger と比べ、 R-17.1 程度低かった。

考察

学習ロスと検証ロスについては、 Ranger に比べて NVLAMB のほうが、今回の学習条件においては適していると考えられる。

レーティングについては、ロスが下がればレーティングが下がるというわけでは必ずしもないという事を表していると考えられる。

まとめ

nnue-pytorch を用いた学習で、 Optimizer を NVLAMB に変更して学習させた場合の、レーティングの変化を調べた。結果、 Ranger に比べてレーティングが伸びなかった。

今後、学習データの生成方法の見直し等を進めていきたいと思う。