tanuki- 2023-11-03 nnue-pytorch halfkp_1024x2-16-32
実験内容
- nnue-pytorch を用い、 halfkp_1024x2-16-32 ネットワークを学習させる。
棋譜生成
| 生成ルーチン | tanuki-棋譜生成ルーチン |
| 評価関数 | Háo |
| 1手あたりの思考 | 深さ最大 9 思考ノード数最大 50,000 ノード |
| 開始局面 | foodgate の 2020 年~ 2021 年の棋譜を使用した。レーティング 3900 以上同士の対局のみ使用した。戦型が角換わりの対局が 10% になるよう調整した。 32 手目までから 1 局面ランダムに選択し、その局面を開始局面とした。ランダムムーブはしなかった。 |
| 生成局面数 | 10 億局面 × 8 セット |
| 生成条件 | 対局は打ち切らず詰みの局面まで学習データに出力した |
シャッフル条件
| 生成ルーチン | tanuki-シャッフルルーチン |
| qsearch() | あり |
| 置換表 | 無効 |
機械学習
| 機械学習ルーチン | nnue-pytorch + やねうら王 https://github.com/nodchip/nnue-pytorch/tree/shogi.2023-10-31.halfkp_1024x2-16-32 |
| 学習モデル | halfkp_1024x2-16-32 |
| 学習手法 | SGD ミニバッチ法 |
| 初期学習率 (lr) | 8.75e-4 |
| 最適化手法 | Ranger |
| 学習率調整手法 | StepLR gamma=0.992 |
| batch-size | 16384 |
| threads | 1 |
| num-workers | 8 |
| gpus | 1 |
| features | HalfKP |
| max_epoch | 500 |
| scaling (kPonanzaConstant) | 361 |
| lambda | 0.5 |
| 勝敗項の教師信号 | 0.999 |
| epoch_size | 10000000 |
レーティング測定
| 対局相手 | tanuki-wcsc32 (マメット・ブンブク) |
| 思考時間 | 持ち時間 300 秒 + 1 手 2 秒加算 |
| 対局数 | 5000 |
| 同時対局数 | 64 |
| ハッシュサイズ | 384 |
| 開始局面 | dlshogi 互角局面集の角換わりの割合が 10% になるよう間引いたもの |
実験結果
機械学習
レーティング測定
対局数=5000 同時対局数=64 ハッシュサイズ=384 開始手数=24 最大手数=320 開始局面ファイル=C:\Jenkins\workspace\TanukiColiseum.2023-04-16\TanukiColiseum\floodgate32-80.adjust_bishop_exchange.sfen NUMAノード数=1 表示更新間隔(ms)=3600000
思考エンジン1 name=YaneuraOu NNUE 7.63 64ZEN2 TOURNAMENT author=by yaneurao exeファイル=C:\Jenkins\workspace\TanukiColiseum.2023-04-16\engine1\source\YaneuraOu-by-gcc.exe 評価関数フォルダパス=D:\hnoda\shogi\eval\tanuki-.nnue-pytorch-2023-11-02 定跡手数=256 定跡ファイル名=no_book 思考ノード数=0 思考ノード数に加える乱数(%)=0 思考ノード数の乱数を1手毎に変化させる=False 持ち時間(ms)=300000 秒読み時間(ms)=0 加算時間(ms)=2000 乱数付き思考時間(ms)=0 スレッド数=1 BookEvalDiff=30 定跡の採択率を考慮する=true 定跡の手数を無視する=true SlowMover=100 DrawValue=-2 BookEvalBlackLimit=0 BookEvalWhiteLimit=-140 FVScale1=16 Depth1=0
思考エンジン2 name=YaneuraOu NNUE 7.63 64ZEN2 TOURNAMENT author=by yaneurao exeファイル=C:\Jenkins\workspace\TanukiColiseum.2023-04-16\engine2\source\YaneuraOu-by-gcc.exe 評価関数フォルダパス=D:\hnoda\tanuki-wcsc32-2022-05-06\eval 定跡手数=256 定跡ファイル名=no_book 思考ノード数=0 思考ノード数に加える乱数(%)=0 思考ノード数の乱数を1手毎に変化させる=False 持ち時間(ms)=300000 秒読み時間(ms)=0 加算時間(ms)=2000 乱数付き思考時間(ms)=0 スレッド数=1 BookEvalDiff=30 定跡の採択率を考慮する=true 定跡の手数を無視する=true SlowMover=100 DrawValue=-2 BookEvalBlackLimit=0 BookEvalWhiteLimit=-140 FVScale2=16 Depth2=0
対局数5000 先手勝ち2465(52.6%) 後手勝ち2222(47.4%) 引き分け313
engine1
勝ち1839(39.2% R-71.1 +-9.8) 先手勝ち980(20.9%) 後手勝ち859(18.3%)
宣言勝ち15 先手宣言勝ち9 後手宣言勝ち6 先手引き分け154 後手引き分け159
engine2
勝ち2848(60.8%) 先手勝ち1485(31.7%) 後手勝ち1363(29.1%)
宣言勝ち17 先手宣言勝ち4 後手宣言勝ち13 先手引き分け159 後手引き分け154
1839,313,2848
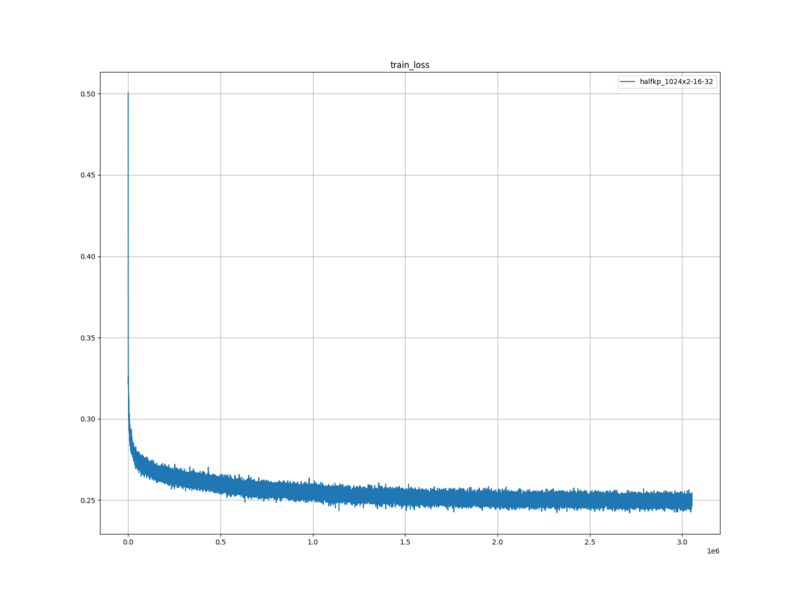
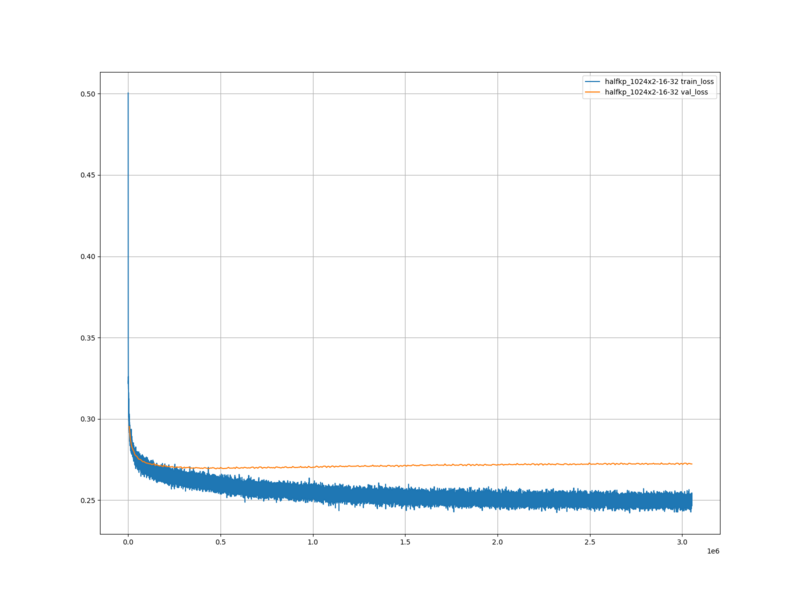
学習ロスは、はじめに急激に下がったあと、緩やかに下がり、一定の値に収束した。
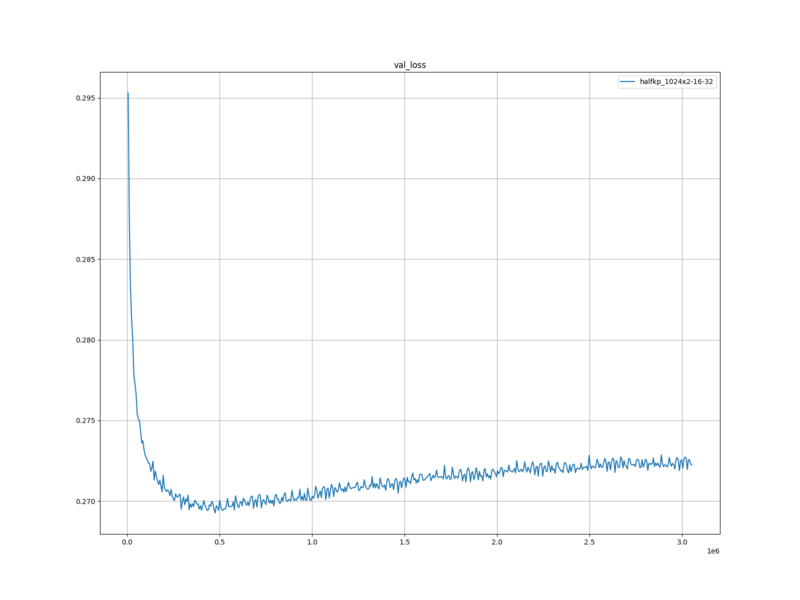
検証ロスは、はじめに急激に下がったあと、緩やかに上昇していった。
halfkp_1024x2-16-32 の評価関数と、 tanuki-wcsc32 評価関数を対局させたところ、レーティングは R-71.1 低く、有意な差があった。
考察
検証ロスが緩やかに上昇していったことから、過学習が起こったと思う。
レーティングが低かったのは、過学習が原因だと思う。 Optimizer に Ranger を使用したことか、学習率が高すぎたことが原因だと思う。
まとめ
nnue-pytorch を用い、 halfkp_1024x2-16-32 ネットワークを学習させた。
結果、過学習によりレーティングが低かった。 Optimizer に Ranger を使用したことか、学習率が高すぎたことが原因だと思う。
また、比較を行うのであれば、 halfkp_1024x2-8-32 ネットワークを使用すべきであった。
次回は、 halfkp_1024x2-8-32 評価関数で、 Warmup + ExponentialLR を試したい。