tanuki- 2022-10-31 nnue-pytorch やねうら王学習率スケジューラー

実験内容

nnue-pytorch を用いた学習で、やねうら王に実装されている newbob 風学習率スケジューラーを用いて学習させる。

棋譜生成

生成ルーチン	tanuki-棋譜生成ルーチン
評価関数	水匠5 FV_SCALE=16
1手あたりの思考	深さ最大 9 思考ノード数最大 50,000 ノード
開始局面	foodgate の 2020 年～ 2021 年の棋譜のうち、レーティング 3900 以上同士の対局の 32 手目までから 1 局面ランダムに選択し、その局面を開始局面としたランダムムーブなし
生成局面数	10 億局面 × 8 セット
生成条件	対局は打ち切らず詰みの局面まで学習データに出力した

シャッフル条件

生成ルーチン	tanuki-シャッフルルーチン
qsearch()	あり
置換表	無効

機械学習

機械学習ルーチン	nnue-pytorch + やねうら王 https://github.com/nodchip/nnue-pytorch/tree/shogi.2022-10-28.sgd
学習モデル	halfkp_256x2-32-32
学習手法	SGD ミニバッチ法
初期学習率 (lr)	1.0
最適化手法	なし
学習率調整手法	newbob 風学習率スケジューラー学習ロスに改善が見られなくなったら、学習率を下げる
batch-size	16384
threads	1
num-workers	8
gpus	1
features	HalfKP
max_epoch	300
scaling (kPonanzaConstant)	361
lambda	0.5
勝敗項の教師信号	0.99
newbob_decay	0.50
epoch_size	10000000
num_epochs_to_adjust_lr	50

レーティング測定

対局相手	tanuki- 2022-10-26 nnue-pytorch GeForce RTX 4090 - Google ドキュメント https://docs.google.com/document/d/1psORyVgOMQly8ul7GZpnD7sWI7-ICLMO962Hcs3FUO8/edit tanuki- 2022-06-07 やねうら王学習部リグレッション調査 V5.33 https://docs.google.com/document/d/1Lup-hHFH2_QWqEfe56obJ6OEwj15P-C0VO6pWV9-vgo/edit?usp=sharing
思考時間	持ち時間 300 秒 + 1 手 2 秒加算
対局数	2000
同時対局数	64
ハッシュサイズ	768
開始局面	たややん互換局面集

実験結果

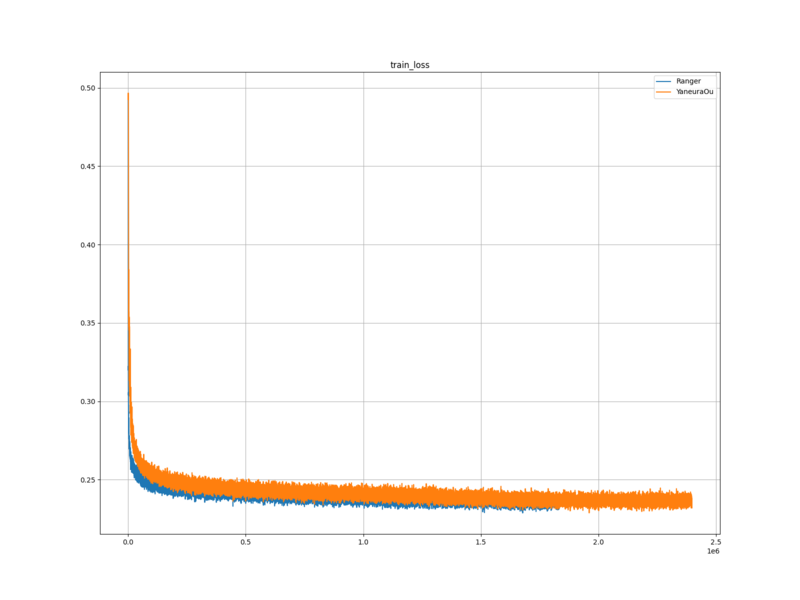
レーティング測定

対局数=2000 同時対局数=64 ハッシュサイズ=768 開始手数=24 最大手数=320 開始局面ファイル=C:\Jenkins\workspace\TanukiColiseum.2022-05-02\TanukiColiseum\taya36_2020-11-06.sfen NUMAノード数=2 表示更新間隔(ms)=3600000

思考エンジン1 name=YaneuraOu NNUE 7.10 64ZEN2 TOURNAMENT author=by yaneurao exeファイル=C:\Jenkins\workspace\TanukiColiseum.2022-05-02\engine1\source\YaneuraOu-by-gcc.exe 評価関数フォルダパス=D:\hnoda\shogi\eval\tanuki-.nnue-pytorch-2022-10-31 定跡手数=256 定跡ファイル名=no_book 思考ノード数=0 思考ノード数に加える乱数(%)=0 思考ノード数の乱数を1手毎に変化させる=False 持ち時間(ms)=300000 秒読み時間(ms)=0 加算時間(ms)=2000 乱数付き思考時間(ms)=0 スレッド数=1 BookEvalDiff=30 定跡の採択率を考慮する=false 定跡の手数を無視する=false SlowMover=100 DrawValue=-2 BookEvalBlackLimit=0 BookEvalWhiteLimit=-140 FVScale1=16

思考エンジン2 name=YaneuraOu NNUE 7.10 64ZEN2 TOURNAMENT author=by yaneurao exeファイル=C:\Jenkins\workspace\TanukiColiseum.2022-05-02\engine2\source\YaneuraOu-by-gcc.exe 評価関数フォルダパス=D:\hnoda\shogi\eval\tanuki-.nnue-pytorch-2022-10-26 定跡手数=256 定跡ファイル名=no_book 思考ノード数=0 思考ノード数に加える乱数(%)=0 思考ノード数の乱数を1手毎に変化させる=False 持ち時間(ms)=300000 秒読み時間(ms)=0 加算時間(ms)=2000 乱数付き思考時間(ms)=0 スレッド数=1 BookEvalDiff=30 定跡の採択率を考慮する=false 定跡の手数を無視する=false SlowMover=100 DrawValue=-2 BookEvalBlackLimit=0 BookEvalWhiteLimit=-140 FVScale2=16

対局数2000 先手勝ち912(52.5%) 後手勝ち826(47.5%) 引き分け262

engine1

勝ち963(55.4% R32.8 +-15.3) 先手勝ち503(28.9%) 後手勝ち460(26.5%)

宣言勝ち40 先手宣言勝ち13 後手宣言勝ち27 先手引き分け133 後手引き分け129

engine2

勝ち775(44.6%) 先手勝ち409(23.5%) 後手勝ち366(21.1%)

宣言勝ち20 先手宣言勝ち8 後手宣言勝ち12 先手引き分け129 後手引き分け133

963,262,775

思考エンジン2 name=YaneuraOu NNUE 7.10 64ZEN2 TOURNAMENT author=by yaneurao exeファイル=C:\Jenkins\workspace\TanukiColiseum.2022-05-02\engine2\source\YaneuraOu-by-gcc.exe 評価関数フォルダパス=D:\hnoda\shogi\eval\regression.v5.33\final 定跡手数=256 定跡ファイル名=no_book 思考ノード数=0 思考ノード数に加える乱数(%)=0 思考ノード数の乱数を1手毎に変化させる=False 持ち時間(ms)=300000 秒読み時間(ms)=0 加算時間(ms)=2000 乱数付き思考時間(ms)=0 スレッド数=1 BookEvalDiff=30 定跡の採択率を考慮する=false 定跡の手数を無視する=false SlowMover=100 DrawValue=-2 BookEvalBlackLimit=0 BookEvalWhiteLimit=-140 FVScale2=16

対局数2000 先手勝ち941(53.7%) 後手勝ち811(46.3%) 引き分け248

engine1

勝ち743(42.4% R-46.5 +-15.4) 先手勝ち403(23.0%) 後手勝ち340(19.4%)

宣言勝ち33 先手宣言勝ち13 後手宣言勝ち20 先手引き分け124 後手引き分け124

engine2

勝ち1009(57.6%) 先手勝ち538(30.7%) 後手勝ち471(26.9%)

宣言勝ち27 先手宣言勝ち12 後手宣言勝ち15 先手引き分け124 後手引き分け124

743,248,1009

学習ロスと検証ロスは、最適化手法に Ranger を使用した場合と比べて下がった。

レーティングは、最適化手法に Ranger を使用した場合と比べて、有意に高かった。一方、やねうら王純正の学習器を使用した場合と比べ、有意に低かった。

考察

halfkp_256x2-32-32 モデルに対しては、 Ranger よりやねうら王純正の newbob 風学習率スケジューラーのほうが適しているという事なのだと思われる。

やねうら王純正の学習器との差は、ミニバッチのサイズと、学習率が下がらなかった際に、チェックポイントに戻るかどうかである。ミニバッチのサイズについては、一般的に大きいほど性能が良くなるとされているため、影響しているとは考えにくい。また、チェックポイントに戻るかどうかについても、あまり大きな差はないように思われる。しかし、明示的な差がこれらしか考えられない。これらについて、調査の必要があると思われる。